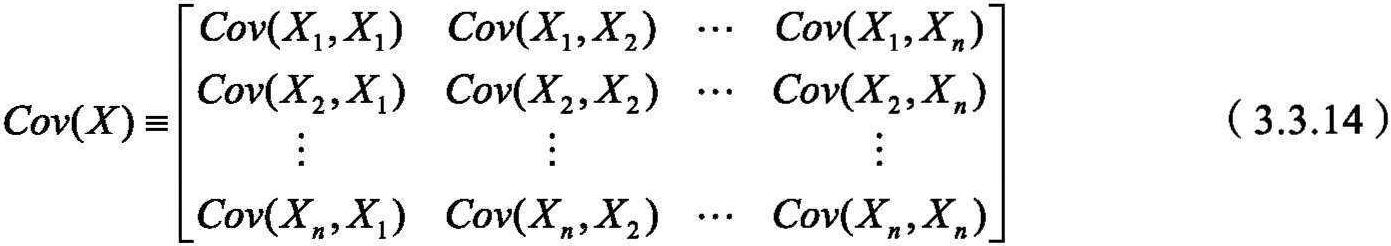
由性質(zhì)3.3.3的證明可知,當X和Y相互獨立時,E{[X-E(X)][Y-E(Y)]}=0,當E{[X-E(X)][Y-E(Y)]}≠0時,X和Y不相互獨立而是存在某種聯(lián)系.定義3.3.1 設(shè)(X,Y)為二維隨機變量,E{[X-E(X)][Y-E(Y)]}存在,則稱其為X和Y的協(xié)方差(covariance),或相關(guān)矩 (correlation moment),記作 (共 4090 字) [閱讀本文] >>
海量資源,盡在掌握
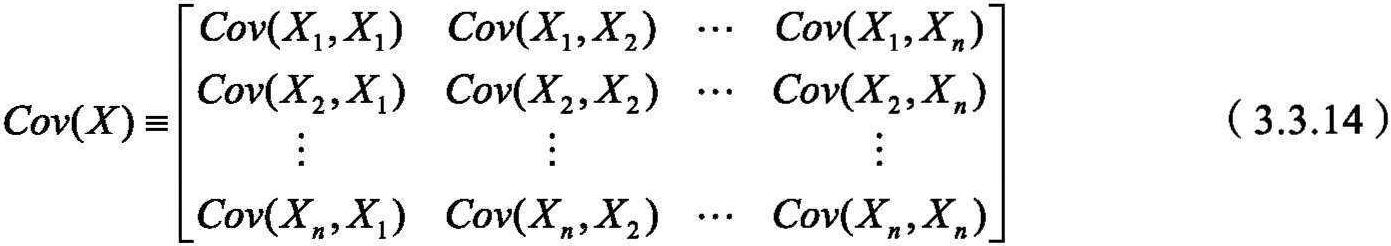
由性質(zhì)3.3.3的證明可知,當X和Y相互獨立時,E{[X-E(X)][Y-E(Y)]}=0,當E{[X-E(X)][Y-E(Y)]}≠0時,X和Y不相互獨立而是存在某種聯(lián)系.定義3.3.1 設(shè)(X,Y)為二維隨機變量,E{[X-E(X)][Y-E(Y)]}存在,則稱其為X和Y的協(xié)方差(covariance),或相關(guān)矩 (correlation moment),記作 (共 4090 字) [閱讀本文] >>